CS231n Lecture 4. Introduction to Neural Networks
대충 정리해요.
_
Scores function/SVM Loss/Data loss + Regularization 까지 배웠으니, 이제 그 뒤로 Optimization을 배운다.
Optimization
loss function을 minimize 시키는 가중치 W를 찾는다.
Gradient Descent
- Numerical gradient : slow, easy to write, approximate
- Analytic gradient : fast, error-prone, exact
In practice: Derive “analytic gradient”
Computational graph
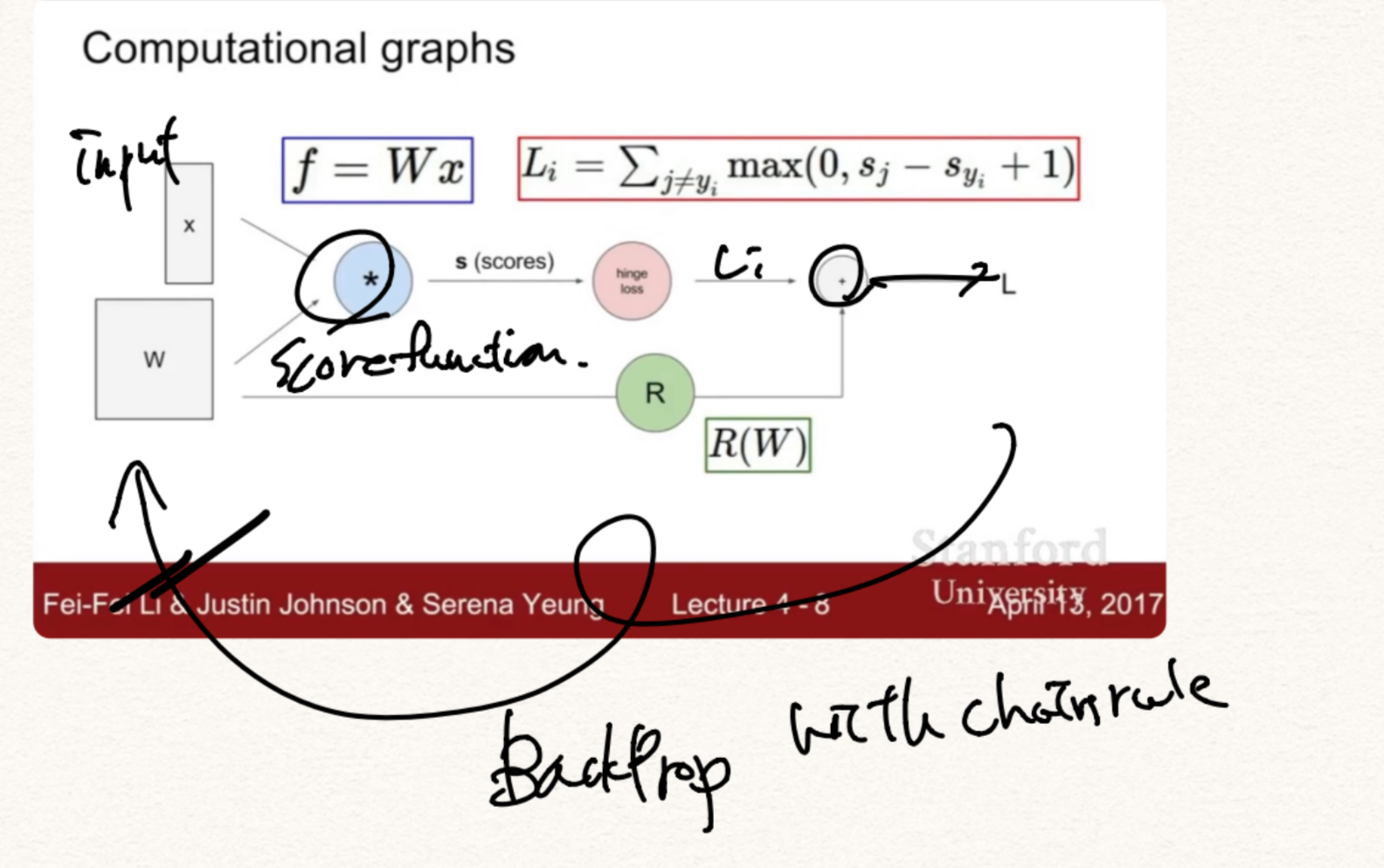
BackProp
전파받은 Gradient를 Local gradient와 곱해서 전달한다.
branch가 나뉘는 곳에서 add는 gradient distributer 처럼 작용하고 max함수는 gradient router처럼 작용한다. 또한 곱은 gradient switcher(scaler)처럼 작용한다.
branch들이 합쳐지는 곳에서는 gradients들이 합해진다.
Vectorized operation
4096차원으로 input, output이 있을때 Gradient를 계산할 때 4096x4096 Jacobian matrix가 필요하다. technical하게 minibatch size로 100을 쓰면 409600x409600 사이즈의 Jacobian matrix가 필요하다. (왜 그런지는 잘 모르겠습니다 ㅠ)
Neural Networks
Activation functions
Sigmoid/Leaky ReLU/Maxout/ELU/ReLU/tahh 등 여러가지 Activation function이 있다.
September 4, 2018
Tags:
cs231n