Mecab을 살펴보자
이 논문(Applying Conditional Random Fields to Japanese Morphological Analysis)을 참고해서 적어본다.
CRFs가 word boundary ambiguity가 존재할 때 어떻게 해결할 수 있는지를 보여준다고 하니, MeCab은 일본어를 word boudnary를 찾기 위해 시작한 프로젝트인 것 같다. 그리고 CRFs가 corpus based나 statistical한 일본어 morphological analysis(형태소 분석이라고 부르면 되려나?)에 있는 문제점들을 해결할 수 있다고 한다. hierarchical tagsets을 위한 flexible feature design이 가능해지고, label bias, length bias의 영향이 적어진다.
1. Introduction
일단 일본어는 중국어처럼 non-segmented language이다. 그래서 word boundary를 찾는 것이 word segmentation을 찾아내는 거나 POS Tagging하는 것에 매우 중요하다. CRFs를 쓰면 이 문제들을 풀어낼 수 있다. HMMs은 generative하기 때문에 hierarchical tagsets들로부터 나온 feature들을 사용하기 힘들다. suffix, prefix 같은 정보들이 예시이다. MEMMs은 label bias나 legnth bias를 해결하기 힘들다.
2. Japanese Morphological Analysis
word boundary를 찾는 가장 쉬운 방법은 character를 token으로 취급해서 Begin/Inside를 tagging하도록 만드는 것이다. (character based BI tagging) 하지만 이 것은 word segmentation에 대해 미리 정보가 있는 lexicon을 활용하기 힘들고, decoding 자체가 정말 많이 느려진다는 데 문제가 있다. (BI Tagging은 candidates를 많이 생성해놓아야 한다)
단어, 품세 페어를 포함하는 lexicon이 없는 것이 아니기 때문에 이를 활용하자는 것이 핵심인 것 같다. (MeCab을 원래 빌드할 떄 사전을 넣는 일이 크기도 하고)
어찌되었든, 일본어 morph analysis를 정리해보면 아래와 같다.
- let \(x\) be an input, unsegmented sentence.
-
let \(y\) be a path, sequence of tuples containing word \(w_i\) and pos \(t_i\)
\[y = [(w1, t1,), ..., (wn, tn)]\] - let \(\mathcal Y(x)\) be a set of candidate paths in a lattice built from the input sentence \(x\) and a lexicon
- let \(\hat y\) be a corrent path by input sentence \(x\)
2.2. Long-Standing Problems
2.2.1. Hierarchical Tagset
일본어 morphological analzer인 ChaSen이랑 JUMAN은 hierarchical structure를 사용한다. CharSen은 IPA tagset을 사용하는데 IPA tagset은 세가지 부분으로 이루어져 있다. POS, conjugation form(cform), conjugate type(ctype). cform이랑 ctype은 단어랑 conjugate에만 지정되고 POS는 4레벨의 서브카테고리가 있다.
명사를 예를 들어서 설명하자면, 명사는 일반 명사, 고유 명사와 같이 나누어지고, 고유명사가 또 다시 사람, 조직, 장소와 같이 나누어진다. 이런 POS tagging에 대해 풀어내야하는 문제는 어떻게 서로 다른 레벨의 정보들을 활용하냐이다. 예를 들어서 특정 suffix는 이름 뒤에 오기 때문에 Name POS란 정보로 분류해내기 편하다.
2.2.2. Label Bias and Length BIas
next state classifier를 활용하는 discriminative model은 대부분 length bias나 label bias가 있을 수 있다. label bias는 아래 그림에서 BOS - A 까지 transition score가 0.6이고, A에서는 C, D로 두개의 transition이 존재하기 때문에 0.6의 확률이 더 줄어들 수 밖에 없다. 결국 \(P(A, D\rvert x) = 0.36\)이 된다. 히지만 B - C의 경로는 B에서 transition이 하나밖에 존재하지 않기 때문에 좋지 않은 경로라고 하여도 \(P(B, E \rvert x) = 0.4\)로 prob은 더 높다.
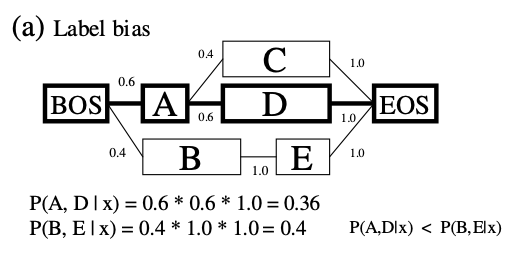
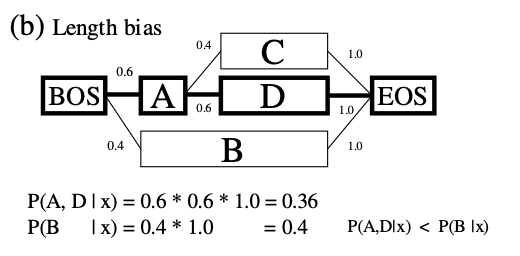
length bias는 말 그대로 path의 length에 관련된 문제이다. 위 그림에서 \(P(A, D \rvert x) = 0.36\)으로 좋은 경로여도 prob이 낮은데, \(P(B\rvert x) = 0.4\)로 안좋은 경로가 prob이 더 높다.
위의 두 예시는 \(P(y\rvert x) = \prod^{n}_{i = 1}p((w_i, t_i)\rvert (w_{i-1}, t_{i-1}))\)과 같은 식을 사용하는 maximum entropy model을 이용할 때의 예시다.
3. Conditional Random Fields
CRFs는 Section 2.2.에 언급된 문제점을 해결할 수 있고 discriminative models이면서, corrleated featrues를 잡을 수 있다. 그래서 hierarchical tagsets으로도 flexible feature design을 할 수 있다. CRFs는 joint prob(\(x\), \(y\))의 single exponential model이므로, label, lenth bias의 문제점을 많이 줄일 수 있다. MEMMs은 sequential combination of exponenetial models이다.
어찌되었든 word boudary ambiguity를 풀기 위해 BI tagging말고 lattice를 활용하기로 했다고 한다. 일본어 morphological anlysis를 위한 CRFs 식은 다음과 같다. (별로 안달라짐)
\[P (y|x) = \frac 1 {Z_x} \exp(\sum_{e i = 1}^{n} \sum_k \lambda_k f_k ((w_{i-1}, t_{i-1}), (w_{i}, t_{i})))\]\(Z_x\)는 normalization factor이다.
\[Z_x = \sum_{y' \in \mathcal y (x)} \exp(\sum_{e i = 1}^{n'} \sum_k \lambda_k f_k ((w'_{i-1}, t'_{i-1}), (w'_{i}, t'_{i})))\]\(f_k ((w_{i-1}, t_{i-1}), (w_{i}, t_{i}))\)는 \(i\), \(i - 1\)번째의 토큰의 feature fuction이다. \(\lambda_k\)는 learned weight이고, \(f_k\)와 연관이 있다고 한다.
근데 이게 원래 많이 쓰이는 CRFs식과는 다르다고 하는데, 그 이유가 MeCab에서 사용하는 CRFs를 사용하는 이유는 word boundary ambiguity를 해결하기 위한 것이고, 따라서 output sequence의 길이가 고정되어 있지 않다.
global feature vector라는 것을 정의하는데 \(\vec F(\vec y, \vec x) = \{F_1 (\vec y, \vec x), ... ,F_K(\vec y, \vec x)\}\)이고, \(F_K(\vec y, \vec x) = \sum^n_{i = 1} f_k ((w_{i-1}, t_{i-1}), (w_{i}, t_{i}))\)이다. 그래서 아래처럼 쓸 수 있다. (근데 벡터 표기해야하는 거 까먹은 게 많은 것 같은데 귀찮으니까 안고칠래..)
\[P(\vec y \rvert \vec x) = \frac 1 {Z_x} exp(\vec \Lambda \vec F(\vec y, \vec x))\]그래서 most probable path \(\hat y\), 즉, 찾고자 하는 경로는 아래와 같아진다.
\[\hat y = \underset {y \in \mathcal Y (x)} {\text{argmax}} P(y\rvert x) = \underset {y \in \mathcal Y (x)} {\text{argmax}} \vec \Lambda \vec F(\vec y, \vec x)\]Viterbi algorithm으로 찾자.
3.1 Parameter Estimation
CRFs는 standard MLE로 training이 가능하다.
\[\hat \Lambda = \underset {\Lambda \in \mathbb R^K} {\text{argmax}} \mathcal L_{\Lambda}, \text where \mathcal L_{\Lambda} = \sum_j \log P(y_j \rvert x_j) = \sum_j [\Lambda F(y_j, x_j) - log(Z_{x_j})]\]이게 optimal point의 first derivative가 0이 된다고 하는데, 이건 Lafferty et al., 2001에서 말하는 convergence를 보장하는 내용을 말하는 것 같다. 위 식을 미분하면 아래처럼 정리가 가능하다.
\[\frac {\partial \mathcal L_{\Lambda}} {\partial \lambda_k} = \sum_j (F_k(y_j, x_j) - E_{P(y \rvert x_j)} F_k(y, y_j)) = O_k - E_k = 0\]위의 차이가 0이 된다. Expectation 은 forward-backward algorithm의 variant로 쉽게 계산될 수 있다고 한다. (이건 진짜 적기 너무 귀찮다.. 논문 다시 보자..)
overfitting을 방지하기 위해 두가지 방식의 regularizaiton을 사용하는데, Gaussian prior (L2-norm), Laplacian prioor(L1-norm)을 사용하면 된다. L1-norm, L2-norm을 사용하는 CRFs를 L1-CRFs, L2-CRFs라고 부른다.
이거도 일단 여기까지 해보고 간단하게 구현해보고 다시 봐야겠다!